低速转向机动性的差动转向控制

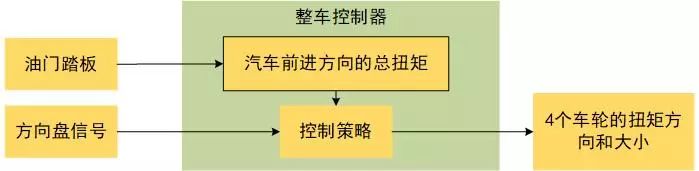
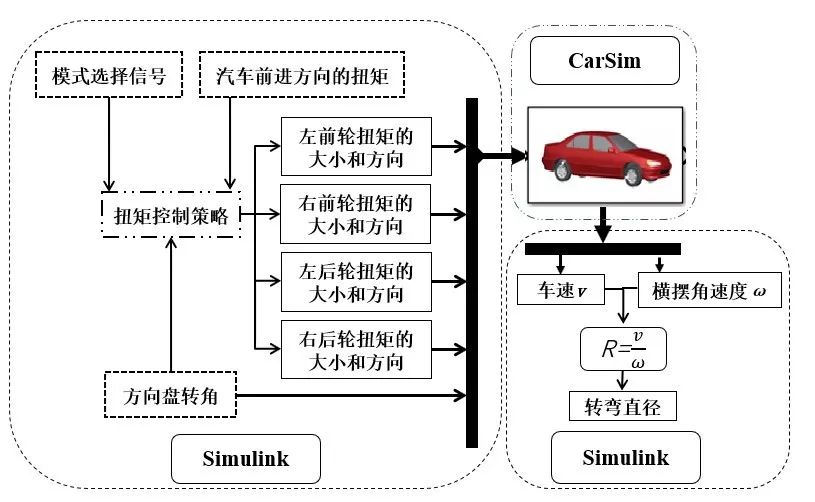
（1）王阳阳：新能源汽车工程中心 智能汽车研究所 智能转向与ADAS设计研究组

（2）江远兴：同济大学 汽车学院 & 智能转向与ADAS设计研究组

（3）刘之光：同济大学 汽车学院 & 智能转向与ADAS设计研究组

摘要：针对常见前轮转向的四轮驱动电动汽车，通过建立四轮驱动汽车的转矩控制策略，调整4个轮毂电机的驱动扭矩，以实现更小的转弯半径，提高低速情况下的转弯机动性。在车速为10 km•h-1时，进行了CarSim仿真和实车试验。结果表明：与普通前轮转向的四轮驱动汽车相比，所设计的3种驱动方式下的转弯直径分别减少了23.0%、2.8%、3.2%，验证了差动控制策略对提高转向机动性的有效性。

1引言

转弯在汽车行车过程中是十分常见的驾驶行为，在低速情况下，或面临小半径转弯时，这对汽车的转向机动性有较高的要求。电机的差动转向对车辆转向时的转向机动性和操纵稳定性均具有改善作用，因此前轮转向和差动转向的复合是提高转向机动性的发展趋势。本文研究采用四轮毂电机的分布式驱动汽车。

国外许多学者对转向机动性进行了研究，Sun等提出了基于差动驱动和差动制动的纵向力分配控制方法，提高了转向性能。Song等通过八自由度车辆模型，设计和验证主动转向与差动转向的模糊控制系统对于转向性能的改善。Tang等针对8电动轮两轴转向汽车，提出了目标输出转矩曲线和两侧转向轮输出控制算法，通过仿真证明差速驱动的可行性。Hajihosseinlu等提出了一种四轮驱动的电子差速器的拓扑结构。基于方向盘角度和加速踏板位置的输入，使用实时功率管理并为4个车轮产生不同的目标扭矩，所提出的算法通过优化操作点滑移率来改善转向特性。Li等通过建立三自由度转向动力学模型，提出了神经网络PID电子差速转速转矩综合控制策略，协调分配四轮毂电机的转矩，改善车辆低速转向转向性能。

国内方面也有许多学者进行了相关研究，陈东等建立非线性十自由度整车模型，利用差动驱动调节纵向力来改善车辆的侧向动力学特性，证明了四轮转向和差动驱动的联合控制有利于提高车辆的转向性能。靳立强等则通过建立多自由度的电动轮汽车模型，提出了以两侧车轮滑移率相同为控制目标的差动控制策略。孙文等提出了通过改变纵向力分配来减小转弯阻力，基于车身稳定性的约束，提高转弯机动性。姜立标等基于八自由度的整车模型，利用模糊PID控制技术以轴间扭矩分配为控制量建立牵引力控制策略，仿真证明该策略能够有效抑制驱动轮滑转，改善汽车转弯性能。

本文结构如下:第二章介绍基于转向机动性的扭矩控制策略。第三章介绍实验过程。第四章介绍试验结果。最后是总结与分析。

2 基于转向机动性的控制策略

A. 模型的控制逻辑

如图1所示，汽车行驶时，驾驶员踩油门踏板，油门踏板的角度信号发送给整车控制器，根据油门踏板与电机的外特性曲线确定汽车前行时沿汽车前进方向的总扭矩。转弯时，驾驶员转动转向盘，转向盘转角信号发送给整车控制器，根据扭矩的控制策略确定4个车轮扭矩的大小和方向。

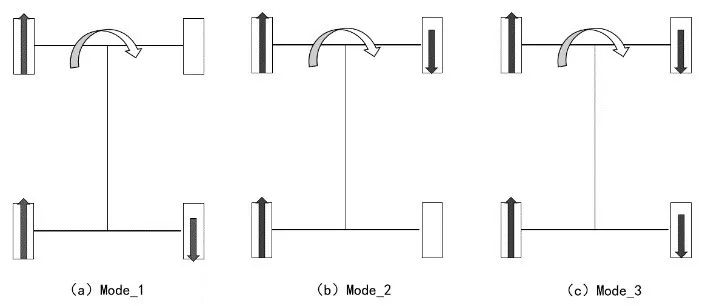
图1. 模型的控制逻辑

B. 扭矩控制模型

当汽车转弯时，外侧车轮的车速大于内侧车轮的车速，为了实现小半径的转弯，基于转向灵活性，根据四轮驱动的特点，设计了3种扭矩分配模型，包括:①外侧车轮驱动+内侧后轮反向输入；②外侧车轮驱动+内侧前轮反向输入；③外侧车轮驱动+内侧车轮反向输入。3种扭矩分配模型示意图如图2所示。为了方便后续区分，3种扭矩分配模型分别定义为Mode_1、Mode_2和Mode_3。

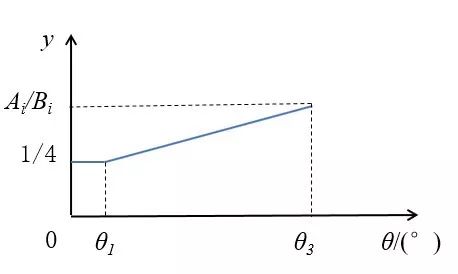
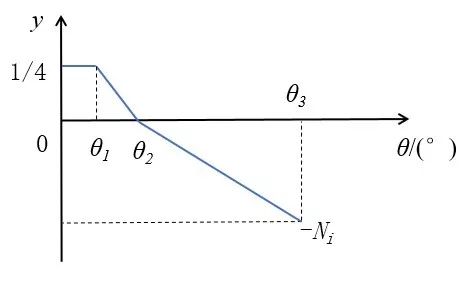
图2. 3种扭矩分配模型

在汽车转弯过程中，转向阻力随着汽车的转向盘转角的增大而增大。因此，基于转向机动性的目的，针对低速汽车转弯，设计了3种扭矩控制策略，通过仿真和试验来证明控制策略的有效性。

驾驶员在操纵转向盘时，无法保证转向盘完全处于零位，对于这3种控制策略，如果不设置转向盘转角阈值，转向盘可能在零位附近波动导致扭矩的方向和大小剧烈波动，不利于汽车的正常行驶。因此，3种扭矩控制策略都在汽车转向盘的零位附近预留一定的转向角阈值。在整个控制策略中，转向盘转角阈值设置为20°。当汽车转向盘转角绝对值小于阈值时，认为这3种扭矩控制策略的差动驱动不起作用；当转向盘转角大于阈值时，这三种扭矩的控制策略与转向盘的变化关系分类讨论。

首先，介绍设计3种扭矩控制策略出现的扭矩变化情况，变化情况分3类，如图3~5所示。图3~5中，θ表示转向盘转角，y 表示扭矩分配系数，即汽车以某个车速前进时，某个车轮的扭矩占汽车前进方向总扭矩的比例，θ1 表示转向盘转角阈值，θ2 表示扭矩分配系数为0的转向盘转角，θ3 表示转向盘的极限转角，i 表示对应的3种模式，Ai（i=1,2,3）表示外侧前轮的最大扭矩分配系数，Bi（i=1,2,3）表示外侧后轮的最大扭矩分配系数，Ni（i=1,2,3）表示内侧车轮的最小扭矩分配系数的绝对值。

如图3所示，在转向盘转角θ1 阈值范围内，每个车轮获得汽车前行扭矩的1/4，即差动不起作用；当转向盘转角θ大于设置的转角阈值θ1时，扭矩分配系数y随着θ线性增加，在达到汽车的转向盘的转角极限θ3 时，扭矩分配系数达到最大，即最大的扭矩分配系数为Ai/Bi（i=1,2,3）。

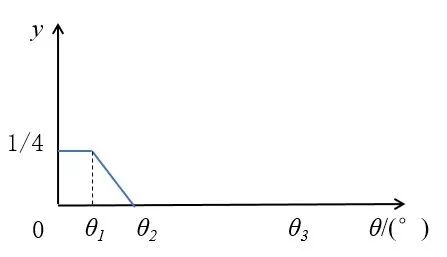
图3. 第一类扭矩分配情况

如图4所示，在转向盘转角的阈值范围内，与第一类相同，不再赘述。当转向盘转角θ大于转向盘转角阈值θ1 时，扭矩分配系数y 随着θ线性减小，直到转向盘转角达到θ2 时，减小为0；转向盘转角θ继续增大，扭矩分配系数保持为0，即不输入扭矩。其中，θ2=40°。

图4. 第一类扭矩分配情况

如图5所示，在θ<θ2时，y 的变化与第二类相同，不再赘述。当θ>θ2 时，y 随着θ的增大继续线性减小，直到θ增大到转向盘的转角极限θ3 时，y减小到最小扭矩分配系数-Ni（i=1,2,3）。

图5. 第一类扭矩分配情况

（1）Mode_1：外侧车轮驱动+内侧后轮反向输入

在该模式下，汽车转弯时，2个外侧车轮的扭矩变化趋势如图3所示。外侧前轮和外侧后轮的最大的扭矩分配系数对应A1 和B1。内侧前轮的扭矩变化趋势如图4所示。内侧后轮的变化趋势如图5所示。此时最小的扭矩分配系数N1=-（1- A1-B1）。

从图3~图5可以看出，对于Mode_1控制策略，在试验过程需要确定的2个标定量，分别是A1和B1。只要确定这2个参数，整个扭矩分配系数与转向盘转角的关系就确定下来。

（2）Mode_2：外侧车轮驱动+内侧前轮反向输入

在该模式下，汽车转弯时，2个外侧车轮的扭矩变化趋势与Mode_1类似，外侧车轮的扭矩变化趋势对应的是图3。外侧前轮和外侧后轮的最大扭矩分配系数分别对应A2和B2。内侧前轮扭矩的变化趋势如图5所示。此时最小的扭矩分配系数N2=-（1- A2- B2）。内侧后轮的变化趋势如图4所示。

从图3~图5可以看出，对于Mode_2控制策略，在试验过程需要确定的两个标定量，分别是A2和B2。只要确定这2个参数，整个扭矩分配系数与转向盘转角的关系就确定下来。

（3）Mode_3：外侧车轮驱动+内侧车轮反向输入

Mode_3的扭矩控制策略与前两种类似，是前两种的综合。外侧车轮的扭矩变化与前两种相同，都采用如图3所示的变化趋势。外侧前轮和外侧后轮的最大扭矩分配系数对应A3和B3。内侧车轮的前后车轮变化是前两种的综合，都采用如图5所示的扭矩变化趋势。内侧前轮的最小扭矩分配系数是-C3，内侧后轮的最小扭矩分配系数是：N3=-（1- A3-B3-C3）。

因此，Mode_3需要确定2个最大扭矩分配系数A3和B3以及一个最小扭矩分配系数的绝对值C3。

C. 算法

根据以上基于转向机动性的扭矩控制策略模型可以看出，模型的输入量是汽车前进方向所需的总扭矩和转向盘转角，输出量是4个车轮扭矩的大小和方向。

为了设置对照试验，在上述提出的3种扭矩控制策略的基础上，同时设置了没有差动转向的参照对象，即四轮的输入扭矩一致。

利用MATLAB/Simulink建立算法逻辑如图6所示。图6中有3个输入量，其中一个输入量是输入参数1~4，用以区分前面3种扭矩控制策略和普通的前轮转向输入，有利于算法的集成化。

图6. 扭矩控制算法逻辑

3试验过程

A. 仿真过程

为了验证算法的可行性，证明基于转向机动性的扭矩控制策略对于减少转弯半径有用，采用了MATLAB/Simulink-CarSim联合仿真。

利用CarSim建立仿真模型时，需要利用到一些汽车参数，对于试验车的部分重要参数如表1所示：

表1 汽车重要的参数

B. 实验过程

对于转弯半径没有传感器可以采用，所以采用滴水法记录汽车的行驶轨迹。由于试验过程中转弯半径不易于测量，因此采用测量轨迹获取转弯直径。一方面，汽车转弯过程中，会发生质量转移，质心位置发生改变；另一方面，驾驶员的存在也会改变质心的位置。因此，汽车质心处无法准确确定，采用汽车前轴中心处和后轴中心处的轨迹代替。实验小车平台如图7所示。

图7 实验车

实验过程如下所示：第一步，将安装在前后轴的容器装满水；第二步，让司机将汽车速度稳定在10 km•h-1，迅速将方向盘调到极限位置，让汽车转弯，司机时刻调整车速，使车速稳定在10 km•h-1，否则重新实验；第三步，利用皮尺将汽车的转弯直径测量下来，时刻注意调整皮尺的位置，保证测量到曲线的最大直径处。

为了实现转向机动性的目的，对于上述提到的3种扭矩控制策略，采用7个标定参数，以最小的转弯直径为目标，进行标定，最终确认标定参数的数值。

4 试验结果

出于安全性考虑，以汽车10km•h-1为仿真试验和实车试验的试验车速，为了验证汽车的极限转弯情况，以汽车转向盘的极限位置为试验转向盘转角。

A. 仿真结果

为了对比分析出实验结果，需要设置参考对象。选择普通的前轮转向工况为参照模式，为了方便后续图表的表示，记为FWS模式。当汽车车速为10 km•h-1，方向盘转角为522°时，利用MATLAB/Simulink-CarSim联合仿真获得质心处的转弯直径，数据记录在表2中。

表1 转弯直径的仿真和实验结果

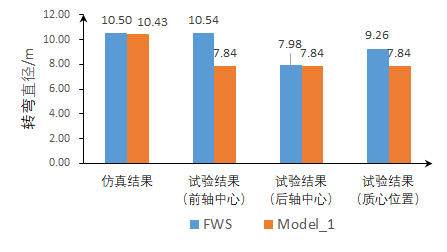
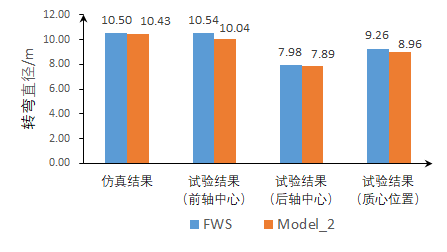
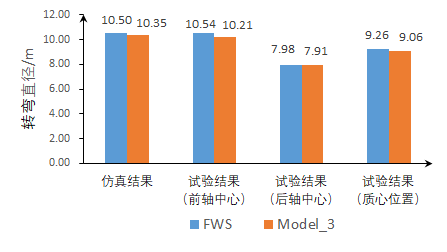
B. 实车实验结果

实车试验过程中，驾驶员先直线加速到10 km•h-1，再将转向盘分别转到左极限和右极限，调整车速稳定在10 km•h-1，分别记录汽车的前轴、后轴中心处的轨迹，利用卷尺测量汽车稳定转弯时的转弯直径，记录下来。每种模式的每个极限位置重复3次，求取前后轴中心处左右极限的平均值，如表2所示。将前后轴的转弯直径求平均值，如表2所示。为了方便分析，将3种模式的转弯直径数据和参考模式（FWS）绘成柱状图，如图8所示。

（a）Mode_1

（b）Mode_2

（c）Mode_3

图8 实验结果对比

最后，将3种模式与参照模式的仿真结果和实验结果对比分析，计算出3种模式与参照模式相比的转弯直径减少百分比，如表3所示。从表3可以看出，实车试验对于减少转弯直径的结果优于仿真结果，尤其是外侧驱动+内侧后轮反向输入的转弯直径与单纯的前轮转向相比，减少了15.31%，效果十分明显。

表3 3种模式的转弯直径减少百分比

5总结与分析

从仿真结果来看，前轮转向+外侧驱动+内侧反向的差动转向，对于转弯直径的减少效果最明显，但只减少了1.5%。

从实验结果来看，前轮转向+外侧驱动+内侧后轮反向的差动转向，对于转弯半径的减少效果最明显。即使是减少效果最不明显的外侧驱动+内侧反向输入的差动转向，也减少了2.16%，因此实车试验结果全面优于仿真结果。

无论是仿真还是实车试验，都证明了差动驱动对于提高汽车的转弯机动性有明显的效果。

本论文已发表于《同济学报》2018年12月刊，该论文同时获得了第14届同济大学研究生学术论坛一等奖和第三届上海-斯图加特汽车及动力技术国际研讨会青年论坛优秀论文。获奖证书如图9